기름방울 실험
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
기름방울 실험은 로버트 A. 밀리컨과 H. 플레처가 1909년 수행한 실험으로, 전하를 띤 기름 방울의 움직임을 통해 전자의 전하량을 측정하는 데 성공했다. 이 실험은 두 개의 전극 사이에 기름 방울을 떨어뜨리고 전기장을 가하여 기름 방울에 작용하는 힘을 분석하는 방식으로 진행되었다. 실험 결과는 전하가 양자화되어 존재한다는 것을 입증하는 중요한 증거가 되었으며, 기본 전하량의 값을 정확하게 측정하는 데 기여했다. 실험 방법은 중력, 부력, 공기 저항, 전기력 등 기름 방울에 작용하는 여러 힘을 고려하여 전하량을 계산하는 방식으로 이루어졌다. 밀리컨은 이 실험을 통해 1923년 노벨 물리학상을 수상했다.
더 읽어볼만한 페이지
- 1909년 과학 - 하버법
하버법은 프리츠 하버가 개발하고 카를 보쉬가 산업화한 암모니아 합성법으로, 대기 중 질소와 수소를 고온, 고압 조건에서 촉매를 사용하여 암모니아를 대량 생산하는 기술이며, 식량 생산에 기여했지만 에너지 소비와 환경 문제도 야기한다. - 1909년 과학 - 알파입자 산란실험
알파 입자 산란 실험은 어니스트 러더퍼드가 수행하여 플럼 푸딩 모델을 뒤엎고 원자핵의 존재를 제안, 현대 원자 물리학의 기초를 다진 실험이다. - 초기 양자역학 - 광전 효과
광전 효과는 빛이 물질에 닿을 때 전자가 방출되는 현상으로, 빛 에너지가 광자라는 덩어리로 양자화되어 있고, 아인슈타인의 광양자 가설로 설명되며, 다양한 기술에 응용되지만 문제도 야기한다. - 초기 양자역학 - 슈테른-게를라흐 실험
슈테른-게를라흐 실험은 은 원자의 자기 모멘트가 양자화되어 있음을 증명하고, 전자의 스핀이 양자화되어 있음을 보여주는 중요한 증거가 되었다. - 물리학 실험 - 슈테른-게를라흐 실험
슈테른-게를라흐 실험은 은 원자의 자기 모멘트가 양자화되어 있음을 증명하고, 전자의 스핀이 양자화되어 있음을 보여주는 중요한 증거가 되었다. - 물리학 실험 - 토리첼리의 실험
토리첼리의 실험은 에반젤리스타 토리첼리가 수행한 실험으로, 수은 기둥의 높이를 측정하여 대기압의 존재를 증명하고 최초의 기압계를 개발하는 데 기여했다.
2. 역사적 배경
전기장 내에서 낙하하는 기름 방울에는 네 가지 주요 힘, 즉 중력, 부력, 공기 저항(스토크스 법칙), 그리고 전기장에 의한 쿨롱력이 작용한다.
1908년부터 시카고 대학교 교수로 재직하던 로버트 A. 밀리컨은 하비 플레처(Harvey Fletcher)의 상당한 도움과 "J. Yinbong Lee 씨의 훌륭한 지원"을 받아 실험 장치를 개선했고, 1913년에 그의 획기적인 연구 결과를 발표했다.[6][7] 하지만 밀리컨이 플레처에게 박사 학위를 주는 조건으로 논문 저자 자격을 포기하도록 강요했다는 주장이 플레처 사후 발견된 문서를 통해 제기되면서 논란이 있다.[8][9] 밀리컨은 그 대가로 벨 연구소에서 플레처의 경력을 쌓는 데 영향력을 행사한 것으로 알려졌다.
밀리컨과 플레처의 기름 방울 실험은 위아래 전극 사이에 있는 유리 상자 안의 기름 방울에 작용하는 힘을 측정하는 것이었다. 전기장을 계산하여 기름 방울의 전하를 측정할 수 있었고, 이를 통해 단일 전자의 전하는 약 -1.592 × 10-19 C이라는 값을 얻었다.
이 실험이 진행될 당시에는 아원자 입자의 존재가 아직 널리 받아들여지지 않았다. 1897년 J. J. 톰슨은 음극선 실험을 통해 음전하를 띤 입자(오늘날의 전자)를 발견했으며, 이 입자의 질량이 수소 원자의 약 1/1837에 불과하다는 것을 알아냈다. 조지 프랜시스 피츠제럴드와 월터 카우프만도 비슷한 실험 결과를 얻었다. 그러나 당시 전기와 자기 현상 대부분은 전하가 마치 빛이 연속적인 파동처럼 여겨졌던 것과 같이 연속적인 양이라는 가정하에 설명되고 있었다.
기본 전하 ''e''는 기본적인 물리 상수 중 하나이므로 그 값을 정확하게 측정하는 것은 매우 중요하다. 밀리컨은 기름 방울 실험을 포함한 여러 업적을 인정받아 1923년 노벨 물리학상을 수상했다.
과거 전하를 연속적인 양으로 생각했던 토머스 에디슨조차 밀리컨과 플레처의 실험 장치를 직접 사용해 본 후 전하가 양자화되어 있다는 사실을 받아들이게 되었다.[10] 이 실험은 이후 여러 세대의 물리학 학생들이 반복했지만, 정확한 결과를 얻기에는 상당히 비용이 많이 들고 까다로운 실험으로 알려져 있다.
한편, 1995년부터 2007년까지 SLAC에서는 쿼크와 같이 분수 전하를 가진 입자를 찾기 위해 컴퓨터를 이용한 자동화된 기름 방울 실험이 여러 차례 수행되었다. 1억 개 이상의 기름 방울을 측정한 후 분수 전하 입자에 대한 증거는 발견되지 않았다.[11]
3. 실험 방법
실험의 정밀도를 높이는 데 있어 가장 큰 어려움 중 하나는 중력 계산에 필요한 기름 방울의 반지름을 정확히 측정하는 것이었다. 기름 방울의 반지름은 약 0.001mm 정도로 매우 작고, 공중에 떠 있는 상태에서 측정해야 했다. 게다가 중력은 반지름의 세제곱에 비례하기 때문에, 반지름 측정 오차가 최종 결과에 미치는 영향이 매우 컸다.
이러한 문제를 해결하기 위해, 밀리컨은 전기장의 방향을 바꾸거나 전기장을 껐을 때 기름 방울이 낙하하는 속도()와 상승하는 속도()를 각각 측정하는 독창적인 방법을 고안했다. 기름 방울은 공기와의 점성 저항 때문에 매우 느린 속도(전기장이 없을 때 약 0.1mm/s)로 움직이며, 짧은 시간 안에 종단 속도에 도달한다.
이렇게 측정된 두 종단 속도(, )와 실험 장치의 제원(전극판 간격, 전위차 등), 그리고 물질의 물리적 성질(기름 밀도, 공기 밀도, 공기 점성 등)을 이용하여 개별 기름 방울의 전하량 ''q''와 반지름 ''r''을 계산할 수 있었다. 이 방법을 통해 밀리컨은 전하가 불연속적인 값을 가지며, 특정 기본 단위(기본 전하량)의 정수배로만 존재한다는 사실, 즉 전하의 양자화를 실험적으로 증명하는 데 성공했다. (상세한 계산 방법과 유도 과정은 하위 섹션에서 다룬다.)
3. 1. 실험 장치
밀리컨과 플레처의 실험 장치는 수평으로 놓인 평행한 금속판 쌍으로 이루어져 있다. 이 판 사이에 전위차를 걸어주면 판 사이 공간에 균일한 전기장을 형성한다. 판들은 서로 절연 물질로 만들어진 링으로 분리되어 있으며, 이 링에는 밝은 빛을 비추기 위한 구멍 3개와 현미경으로 내부를 관찰하기 위한 구멍 1개가 있다.
판 위쪽 챔버에는 분무기를 이용해 미세한 기름 방울 안개를 뿌린다. 이때 사용되는 기름은 주로 진공 장치에 쓰이는 종류로, 증기압이 매우 낮기 때문에 선택되었다. 증기압이 낮은 기름을 쓰는 이유는 일반적인 기름의 경우 실험 중 광원의 열 때문에 증발하여 기름 방울의 질량이 변할 수 있기 때문이다. 기름 방울 중 일부는 분무기 노즐을 통과할 때 발생하는 마찰로 인해 전하를 띠게 되었다. 또는 X선관과 같은 이온화 방사선원을 이용하여 인위적으로 기름 방울을 대전시킬 수도 있다.
대전된 기름 방울이 판 사이의 공간으로 들어가고 대전되었으므로, 판에 걸린 전압을 조절하여 방울을 상승시키거나 하강시킬 수 있다.
전기장 내에서 낙하하는 기름 방울에 작용하는 힘은 다음과 같다.
# 중력:
# 부력:
# 공기 저항 (스토크스 법칙):
# 전계에 의한 쿨롱력:
각 변수는 다음을 의미한다.
실험에서 중력과 전기력이 평형을 이루는 조건을 찾더라도, 정밀도를 확보하는 데 있어 문제 중 하나는 중력 계산에 필요한 기름 방울 반지름 측정의 정확성이다. 기름 방울의 반지름은 약 0.001mm 정도로 매우 작고, 공중에 떠 있는 상태에서 측정해야 한다. 게다가 중력은 반지름의 세제곱에 비례하므로, 반지름 측정 오차가 최종 결과에 큰 영향을 미치게 된다.
이러한 어려움을 피하기 위해, 밀리컨은 전기장의 방향을 바꾸었을 때 기름 방울의 낙하 속도 (전기장이 중력과 반대 방향일 때)과 (전기장이 중력과 같은 방향일 때 또는 전기장이 없을 때)를 각각 측정하여 전하량 ''q''를 구하는 방법을 사용했다.[1] 기름 방울은 점성 저항 때문에 매우 느려서(전기장이 없을 때 약 0.1mm/s) 빠르게 종단 속도에 도달한다. 예를 들어 종단 속도가 10mm/s라도 약 1/1000초 내외로 속도 평형에 도달하는 것으로 생각된다.
계산의 편의를 위해 중력과 부력 항을 합쳐 유효 밀도 로 정의한다.
결과적으로 전하량 ''q''는 다음과 같이 구해지며, 이는 두 속도의 차이(), 즉 전기장의 변화에 비례함을 알 수 있다.
또한, 이 측정값으로 기름 방울의 반지름 ''r''도 다음과 같이 계산할 수 있다.
반지름 ''r''은 전기장의 세기 ''U''에 직접적으로 의존하지 않으며, 두 속도의 합()의 제곱근, 즉 전기장이 없을 때의 속도와 관련된 값에 비례한다.
3. 2. 측정 과정
측정은 먼저 전기장이 꺼진 상태에서 기름 방울이 전극판 사이로 떨어지도록 하는 것으로 시작한다. 기름 방울은 챔버 안의 공기와의 마찰 때문에 빠르게 종단 속도에 도달한다. 이후 전기장을 켜면, 전하를 띤 일부 방울은 위쪽으로 작용하는 전기력 (''F''E)이 아래쪽 중력 (''F''g)보다 클 경우 상승하기 시작한다. 관찰하기 적합한 방울 하나를 선택하고 전압을 조절하여 시야 중앙에 유지시킨다. 이 과정에서 다른 방울들은 계속 낙하하도록 둔다. 선택된 방울 하나로 실험을 진행한다.기름 방울이 전기장 없이 자유 낙하할 때의 종단 속도 ''v''1을 측정한다. 이때 방울에 작용하는 공기 저항(항력) ''F''u는 스토크스 법칙을 이용하여 다음과 같이 계산할 수 있다.
:
여기서 ''η''는 공기의 점성, ''r''은 방울의 반지름이다.
방울의 무게 '''''w'''''는 부피 ''D''에 밀도 ''ρ''와 중력 가속도 '''''g'''''를 곱한 값이다. 실험에서 고려해야 할 것은 공기 중에서 측정되는 겉보기 무게인데, 이는 실제 무게에서 부력(방울이 밀어낸 공기의 무게만큼 발생)을 뺀 값이다. 방울이 완벽한 구형이라 가정하면 겉보기 무게는 다음과 같이 쓸 수 있다.
:
여기서 ''ρ''air는 공기의 밀도이다.
종단 속도에 도달하면 방울은 가속도 없이 등속 운동하므로, 작용하는 총 힘(알짜힘)은 0이 된다. 따라서 위쪽으로 작용하는 항력 ''F''u와 아래쪽으로 작용하는 겉보기 무게 의 크기는 같다(). 이 관계식으로부터 방울의 반지름 ''r''을 계산할 수 있다.
:
''r'' 값이 구해지면 겉보기 무게 도 계산할 수 있다.
이제 전기장을 다시 켜면, 방울의 전하 ''q''와 전기장 ''E''에 의해 전기력 ''F''E가 작용한다.
:
평행한 전극판 사이의 전기장 ''E''는 전위차 ''V''와 판 사이의 거리 ''d''를 이용하여 다음과 같이 나타낸다.
:
기름 방울의 전하 ''q''를 구하는 한 방법은 전압 ''V''를 조절하여 방울이 공중에 정지하도록 하는 것이다. 이때는 전기력 ''F''E와 겉보기 무게 가 평형을 이룬다(). 하지만 스토크스 법칙을 사용하지 않고 방울의 질량을 결정하기는 어려우므로, 이 방법으로 ''F''E를 정확히 결정하기는 어렵다.
더 실용적인 방법은 전압 ''V''를 약간 높여 기름 방울이 새로운 종단 속도 ''v''2로 상승하도록 하는 것이다. 이때 방울에 작용하는 힘들의 관계는 다음과 같다.
:
이 식을 이용하여 전하 ''q''를 계산할 수 있다.
전기장 내에서 움직이는 기름 방울에 작용하는 힘은 다음과 같이 정리할 수 있다.
# 중력:
# 부력:
# 공기 저항 (스토크스 법칙):
# 전기력 (쿨롱력):
각 변수의 의미는 다음과 같다.
실험의 정밀도를 확보하기 위한 과제 중 하나는 중력 계산에 필요한 기름 방울의 반지름 ''r''을 정밀하게 측정하는 것이다. 기름 방울의 반지름은 대략 0.001mm 정도로 매우 작으며, 공중에 부유하는 상태에서 측정해야 한다. 게다가 중력은 반지름의 세제곱에 비례하므로, 반지름 측정 오차가 결과에 미치는 영향이 크다.
이 어려움을 피하기 위해, 밀리컨은 전기장의 방향을 바꾸었을 때 방울이 하강하는 속도()와 상승하는 속도()를 각각 측정하여 전하량을 구하는 방법을 고안했다. 기름 방울의 종단 속도는 매우 느려서(전기장이 없을 때 약 0.1mm/s), 공기 저항으로 인해 아주 짧은 시간 안에 종단 속도에 도달한다.
계산을 간편하게 하기 위해 중력과 부력의 효과를 합친 유효 밀도 (여기서 는 공기 밀도)를 사용하면, 전하량 ''q''와 반지름 ''r''은 최종적으로 다음과 같은 식으로 표현된다.
이 결과로부터 전하량 ''q''는 두 속도의 차이()와 합의 제곱근()의 곱에 비례하고, 반지름 ''r''은 두 속도의 합()의 제곱근에 비례함을 알 수 있다. 특히 반지름은 전기장()에 의존하지 않는다.
3. 3. 전하량 계산
실험 초기에는 전기장이 없는 상태에서 기름 방울이 두 개의 평행한 금속판 사이로 떨어지게 한다. 기름 방울은 챔버 안의 공기와의 마찰 때문에 빠르게 종단 속도에 도달한다. 이후 전기장을 가하면, 충분히 강한 전기장 하에서는 전하를 띤 일부 기름 방울이 위쪽으로 상승하기 시작한다. 이는 위쪽으로 작용하는 전기력(FE)이 아래쪽으로 작용하는 중력(Fg)보다 크기 때문이다. 관찰하기 적합한 기름 방울 하나를 선택하고, 전압을 조절하여 이 방울을 시야 중앙에 유지하면서 다른 방울들은 떨어지도록 한다. 선택된 단일 방울로 실험을 진행한다.먼저 전기장이 없을 때 기름 방울이 떨어지는 종단 속도 ''v''1을 측정한다. 이때 방울에 작용하는 항력은 스토크스 법칙을 이용하여 계산할 수 있다.
:
여기서 ''v''1은 전기장이 없을 때 방울의 종단 속도, ''η''는 공기의 점성, ''r''은 방울의 반지름이다.
방울의 무게 ''w''는 부피 ''D''에 밀도 ''ρ''와 중력 가속도 ''g''를 곱한 값이다. 하지만 실험에서는 공기 중에서의 겉보기 무게가 필요하다. 겉보기 무게는 실제 무게에서 방울이 밀어낸 공기의 무게만큼의 부력을 뺀 값이다. 방울이 완벽한 구형이라고 가정하면, 겉보기 무게 ''w'''는 다음과 같다.
:
여기서 ''ρ''는 기름의 밀도, ''ρ''air는 공기의 밀도이다.
종단 속도에서는 방울의 가속도가 0이므로, 방울에 작용하는 알짜힘은 0이다. 즉, 항력 ''F''u와 겉보기 무게 ''w'''가 평형을 이룬다 (). 이 관계식으로부터 방울의 반지름 ''r''을 구할 수 있다.
:
:
반지름 ''r''이 계산되면, 방울의 겉보기 무게 ''w'''도 계산할 수 있다.
이제 전기장을 다시 켜면, 기름 방울에는 전기력 ''F''E가 추가로 작용한다.
:
여기서 ''q''는 기름 방울의 전하량이고, ''E''는 평행판 사이의 전기장이다. 평행판 사이의 전기장은 다음과 같이 주어진다.
:
여기서 ''V''는 두 판 사이의 전위차이고, ''d''는 판 사이의 거리이다.
전하량 ''q''를 구하는 한 가지 방법은 전위차 ''V''를 조절하여 기름 방울이 공중에 정지하도록 하는 것이다. 이 경우, 전기력 ''F''E와 겉보기 무게 ''w'''가 평형을 이룬다 (). 즉, 이므로, 전하량은 다음과 같이 계산된다.
:
더 실용적인 방법은 전위차 ''V''를 조절하여 기름 방울이 새로운 종단 속도 ''v''2로 상승하도록 하는 것이다. 이때 방울에 작용하는 힘들의 평형 방정식은 다음과 같다 (상승 방향을 +로 가정).
:
:
여기서 이므로, 위 식에 대입하고 정리하면 다음과 같다.
:
:
이 식에 위에서 구한 반지름 ''r''의 식 을 대입하여 ''q''를 속도, 전압 및 물질 상수들로만 표현할 수도 있다.
밀리컨은 이 실험을 통해 측정한 여러 기름 방울의 전하량 ''q''가 항상 어떤 기본 전하량의 정수배라는 사실을 발견했고, 이 기본 전하량이 바로 기본 전하량 ''e'' 임을 밝혔다.
실험에 사용되는 주요 변수들은 다음과 같다.
4. 실험 결과 및 의의
밀리컨과 플레처의 실험은 두 개의 전극 사이에 위치한 유리 챔버 안의 기름 방울에 작용하는 힘을 정밀하게 측정하는 방식으로 진행되었다. 전기장의 세기를 조절하며 기름 방울의 움직임을 관찰하여 방울이 띤 전하량을 계산할 수 있었고, 이를 통해 단일 전자가 가지는 기본 전하량 ''e''의 값을 측정하는 데 성공했다. 그들이 측정한 초기 값은 약 -1.592 × 10-19 C이었다.[7]
이 실험이 수행될 당시(1910년대 초반)에는 아원자 입자의 존재가 아직 과학계 전반에 보편적으로 받아들여지지 않았다. 1897년 J. J. 톰슨이 음극선 실험을 통해 전자를 발견하고 그 질량이 수소 원자의 약 1/1837에 불과하다는 것을 밝혔지만[7], 조지 프랜시스 피츠제럴드나 월터 카우프만 등의 유사한 연구 결과에도 불구하고[7] 당시 전기와 자기 현상은 대부분 전하가 마치 물처럼 연속적인 양이라는 가정하에 설명되고 있었다. 이는 마치 빛이 실제로는 광자라는 불연속적인 입자의 흐름임에도 불구하고 많은 경우 연속적인 파동으로 취급하여 설명하는 것과 유사한 상황이었다.[7]
밀리컨의 기름방울 실험은 이러한 기존의 통념을 깨고 전하가 불연속적인 특정 기본 단위(기본 전하 ''e'')의 정수배로만 존재한다는 사실, 즉 전하의 양자화(quantization)를 명백하게 실험적으로 증명했다는 점에서 매우 중요한 과학사적 의의를 갖는다. 기본 전하 ''e''는 자연계의 기본적인 물리 상수 중 하나로, 그 정확한 값을 아는 것은 물리학의 발전에 필수적이다. 밀리컨은 이 실험을 포함한 여러 업적을 인정받아 1923년 노벨 물리학상을 수상했다.[7]
이 실험 결과는 당대의 저명한 발명가 토머스 에디슨과 같이 전하를 연속적인 것으로 생각했던 이들에게도 큰 영향을 주어 생각을 바꾸게 만들었다.[10] 기름방울 실험은 이후 여러 세대의 물리학 학생들에게 전하의 양자화를 직접 확인하는 중요한 교육 실험으로 자리 잡았지만, 정밀한 결과를 얻기 위해서는 상당한 비용과 노력이 필요하다.[7]
한편, SLAC에서는 1995년부터 2007년까지 이 실험의 원리를 응용한 컴퓨터 자동화 실험을 통해 쿼크와 같이 기본 전하보다 작은 분수 전하를 가진 입자를 찾으려는 시도가 있었으나, 1억 개 이상의 기름 방울을 측정한 결과 그러한 입자의 존재 증거는 발견되지 않았다.[11]
2019년 국제단위계(SI) 개정을 통해 기본 전하량 ''e''의 값은 더 이상 실험적으로 측정되는 값이 아니라, 정확히 1.602176634 × 10-19 C으로 정의되었다. 이는 다른 기본 상수들과의 관계를 통해 킬로그램과 같은 다른 기본 단위를 정의하는 기준으로 사용된다.
밀리컨이 초기에 측정한 값은 현재 받아들여지는 값과 약간의 차이가 있었다. 밀리컨이 노벨상 강연에서 제시한 값은 4.774(5) × 10-10 statC (1.5924(17) × 10-19 C)이었는데,[13] 이는 2014년 CODATA 권장값인 1.6021766208(98) × 10-19 C[12]와 비교하면 약 1% 미만의 차이지만, 밀리컨이 제시한 표준 오차 범위를 고려하면 통계적으로 유의미한 차이였다. 이후 X선 실험이나[14] 전자 회절[15] 등 다른 방법을 이용한 후속 연구들에서 밀리컨의 초기 값보다 약간 더 높은 값들이 측정되었고, 이러한 차이는 공기의 점성 계수 값의 부정확성 등 실험 조건의 문제에서 비롯된 것으로 밝혀졌다. 결국 여러 차례의 정밀한 측정과 검토를 거쳐 기본 전하량 값은 점차 수정되어 현재의 값에 이르게 되었다.
5. 비판과 논란
로버트 A. 밀리컨은 1908년부터 시카고 대학교 교수로 재직하면서 하비 플레처(Harvey Fletcher)의 상당한 도움을 받았고,[6] "J. Yinbong Lee 씨의 훌륭한 지원"과 함께 장치를 개선하여 1913년에 그의 획기적인 연구를 발표했다.[7] 그러나 플레처가 사망한 후 발견된 그의 논문에는, 밀리컨이 플레처에게 박사 학위를 받는 조건으로 실험 결과 발표 논문의 저자 자격을 포기하도록 강요했다는 내용이 담겨 있어 논란이 되었다.[8][9] 그 대가로 밀리컨은 자신의 영향력을 이용해 벨 연구소에서 플레처의 경력을 지원했다고 전해진다.
밀리컨의 실험 결과 자체에 대한 비판도 제기되었다. 물리학자 제럴드 홀튼(1978)은 밀리컨이 실험 노트에 기록된 모든 측정값을 최종 결과에 포함하지 않았다는 점을 지적하며 문제를 제기했다. 홀튼은 밀리컨이 특별한 이유 없이 실험에서 얻어진 많은 기름 방울 데이터를 결과에서 제외했다고 주장했다.[16]
이러한 주장에 대해 콜로라도 대학교의 고에너지 물리학 실험가이자 과학 철학자인 앨런 프랭클린은 밀리컨의 데이터 제외가 최종적인 기본 전하 ''e'' 값 자체에는 실질적인 영향을 미치지 않았지만, 이 추정치 주변의 통계적 오차를 줄이는 효과를 가져왔다고 반박했다. 즉, 밀리컨은 데이터 선별을 통해 자신의 측정 결과가 실제보다 더 정밀한 것처럼 보이게 했을 수 있다는 것이다. 프랭클린에 따르면, 밀리컨이 제외한 데이터를 모두 포함했다면 평균의 표준 오차는 2% 이내가 되었을 것이며, 이는 여전히 당시 누구보다 정확한 측정이었지만, 약간 더 큰 불확실성으로 인해 물리학계 내에서 그의 결과에 대한 더 많은 이견을 낳았을 수 있다.[16] 프랭클린은 밀리컨이 데이터에 "성형 수술"을 했을 수 있다는 결론으로 밀리컨의 측정을 지지했다.
한편, 데이비드 굿스타인은 밀리컨이 보관한 상세한 실험 노트를 직접 조사한 결과, 밀리컨은 보고서에서 "완전한 일련의 관찰"을 거친 방울만을 포함했으며, 이 완전한 측정 그룹 내에서는 어떤 방울도 임의로 제외하지 않았다고 명확히 밝혔다고 주장했다.[17][18] 굿스타인에 따르면, 완전한 관찰을 생성하지 못한 데이터가 제외된 이유에는 장치 설정 문제, 기름 방울 생성의 어려움, 실험 환경(대기)의 영향 등이 포함되어 있었으며, 밀리컨 스스로 이러한 요인들이 특정 측정의 신뢰도를 떨어뜨린다고 판단했다는 것이다.
6. 현대적 의의 및 영향
기본 전하 ''e''는 기본적인 물리 상수 중 하나이므로 그 값의 정확성은 매우 중요하다. 밀리컨은 기름방울 실험을 포함한 여러 공로를 인정받아 1923년 노벨 물리학상을 수상했다.[7]
이 실험은 과학계에 큰 영향을 미쳤다. 이전까지 전하를 연속적인 양으로 생각했던 토머스 에디슨과 같은 과학자들도 밀리컨과 플레처의 장치를 함께 사용해 본 후 전하가 양자화되어 있다는 사실을 받아들이게 되었다.[10] 이 실험은 이후 여러 세대의 물리학 학생들에게 중요한 실험으로 교육되어 왔지만, 실험 장비가 비싸고 정확한 결과를 얻기 어렵다는 단점도 있다.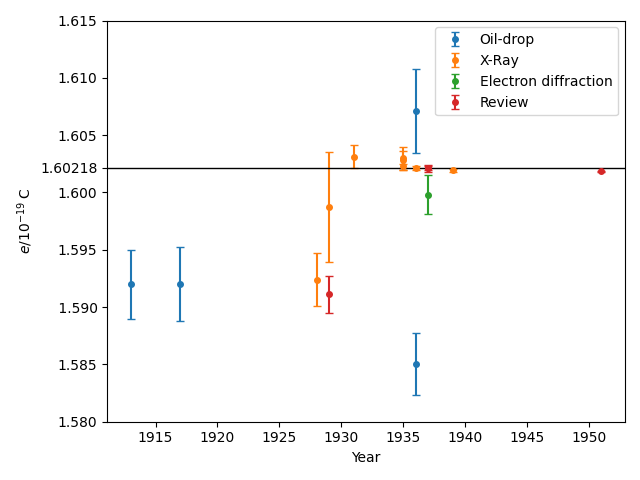
1995년부터 2007년까지 SLAC에서는 밀리컨의 실험과 유사한 원리를 이용하여 쿼크와 같은 분수 전하를 가진 입자를 찾으려는 컴퓨터 자동화 실험이 수행되었지만, 1억 개 이상의 방울을 측정한 결과 분수 전하 입자에 대한 증거는 발견되지 않았다.[11]
한편, 물리학자 리처드 파인만은 1974년 캘리포니아 공과대학교(Caltech) 졸업 연설에서 밀리컨의 실험 결과에 대해 비판적인 시각을 제시했다. 그는 밀리컨이 실험 당시 사용했던 공기의 점성 값이 부정확하여 전자 전하 측정값에 오류가 있었음을 지적했다. 또한, 파인만은 밀리컨 이후 발표된 전자 전하 측정값들이 점진적으로 현재 알려진 값으로 수렴해가는 경향을 보이는데, 이는 과학자들이 기존의 권위 있는 결과(밀리컨의 값)와 크게 다른 값을 얻었을 때 실험 자체에 오류가 있다고 가정하고 결과를 폐기하거나 수정하려는 확증 편향이 작용했을 수 있음을 시사한다고 주장했다.[19][20] 파인만의 이러한 지적은 과학 연구 과정에서 발생할 수 있는 인간적인 오류와 편향의 가능성을 보여주는 사례로 종종 인용된다.
7. 추가 설명: 파인만의 지적
물리학자 리처드 파인만은 1974년 캘리포니아 공과대학교(Caltech) 졸업 연설에서 밀리컨 실험 결과와 관련된 흥미로운 관찰을 제시했다. 이 내용은 1985년 ''파인만 씨, 농담도 잘하시네!''와 1999년 ''사물을 이해하는 즐거움''에도 실렸다.[19][20] 파인만은 밀리컨이 측정한 전자의 전하 값이 당시 사용했던 공기의 점성 계수 값이 부정확했기 때문에 현재 알려진 값과 약간의 차이가 있었다고 지적했다.
더 나아가 그는 밀리컨 이후 수행된 전자 전하 측정 연구들의 결과를 시간 순서대로 살펴보면 흥미로운 경향을 발견할 수 있다고 말했다. 후속 연구 결과들이 점차 밀리컨의 값보다 조금씩 큰 값으로 나타나면서 점진적으로 현재의 정확한 값에 수렴해갔다는 것이다.
파인만은 이러한 현상이 발생한 이유에 대해, 연구자들이 무의식적으로 기존의 권위 있는 결과(밀리컨의 값)에 부합하는 결과를 선호하는 경향, 즉 확증 편향과 유사한 심리가 작용했을 수 있다고 설명했다. 그는 다음과 같이 말했다: "우리는 우리 자신을 속이는 몇 가지 방식들을 다루는 방법에 대해 경험을 통해 많은 것을 배웠습니다. 한 가지 예로, 밀리컨은 낙하하는 기름 방울을 이용한 실험으로 전하량을 측정했고, 현재 우리가 옳지 않다고 알고 있는 답을 얻었습니다. 그것은 약간 빗나갔는데, 그가 공기의 점성에 대한 부정확한 값을 가지고 있었기 때문입니다. 밀리컨 이후의 전자 전하 측정 역사를 살펴보는 것은 흥미롭습니다. 시간의 함수로 그것들을 플롯하면, 하나는 밀리컨의 것보다 약간 크고, 다음 것은 그보다 약간 더 크고, 그 다음 것은 그보다 약간 더 커서, 마침내 더 높은 숫자로 수렴한다는 것을 알 수 있습니다. 왜 그들은 즉시 새로운 숫자가 더 높다는 것을 발견하지 못했을까요? 과학자들이 부끄러워하는 일인데, 바로 이런 역사 때문입니다. 사람들은 이런 식으로 행동한 것이 분명합니다. 밀리컨의 값보다 너무 높은 숫자를 얻으면, 그들은 뭔가 잘못되었음에 틀림없다고 생각하고, 뭔가 잘못되었을 이유를 찾아낼 것입니다. 밀리컨의 값에 가까운 숫자를 얻었을 때는 그렇게 열심히 찾아보지 않았습니다. 그래서 그들은 너무 벗어난 숫자들을 제거하고, 그와 같은 다른 일들을 했습니다..."
파인만의 이러한 지적은 과학 연구 과정에서 발생할 수 있는 인간적인 편향의 가능성을 보여주는 사례로 종종 인용된다.
참조
[1]
논문
The isolation of an ion, a precision measurement of its charge, and the correction of Stokes's law
https://authors.libr[...]
[2]
웹사이트
American Physical Society to commemorate University of Chicago as historic physics site in honor of Nobel laureate Robert Millikan at University of Chicago
http://www-news.uchi[...]
2006-11-28
[3]
웹사이트
UChicago Breakthroughs: 1910s
https://www.uchicago[...]
2019-07-31
[4]
웹사이트
Work of physicist Millikan continues to receive accolades
http://chronicle.uch[...]
2007-01-04
[5]
웹사이트
The Nobel Prize in Physics 1923
https://www.nobelpri[...]
2023-10-15
[6]
논문
The Oil Drop Experiment: A Rational Reconstruction of the Millikan–Ehrenhaft Controversy and Its Implications for Chemistry Textbook
http://www.umich.edu[...]
[7]
논문
On the Elementary Electrical Charge and the Avogadro Constant
[8]
논문
Remembering The Oil Drop Experiment
2007-05
[9]
논문
My Work with Millikan on the Oil-drop Experiment
1982-06
[10]
서적
Nobel Awards Winner Physics
https://books.google[...]
Pinnacle Technology
2009-03-11
[11]
웹사이트
SLAC – Fractional Charge Search – Results
http://www.slac.stan[...]
Stanford Linear Accelerator Center
2007-01
[12]
웹사이트
2014 CODATA Values: Older values of the constants
http://physics.nist.[...]
NIST
2015-06-25
[13]
간행물
The electron and the light-quant from the experimental point of view
http://nobelprize.or[...]
1924-05-23
[14]
논문
Probable Values of the General Physical Constants
1929-07-01
[15]
논문
On the values of fundamental atomic constants
1937-06
[16]
논문
Millikan's Oil-Drop Experiments
[17]
논문
In defense of Robert Andrews Millikan
http://calteches.lib[...]
Caltech Office of Public Relations
[18]
논문
In Defense of Robert Andrews Millikan
http://calteches.lib[...]
[19]
웹사이트
Cargo Cult Science
http://www.lockhaven[...]
California Institute of Technology
[20]
서적
"Surely you're joking, Mr. Feynman!": adventures of a curious character
https://books.google[...]
W. W. Norton & Company
1997-04-01
[21]
웹사이트
CODATA Value: elementary charge
http://physics.nist.[...]
NIST
2021-04-22
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
